If you remember little else from high school geometry, you probably remember the Pythagorean Theorem: The square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. Or, to put it in a formula:
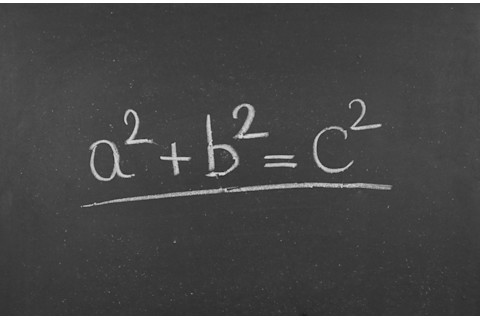
(Credit: pedica018/Shutterstock)
pedica018/Shutterstock
The formula comes in handy in construction, land surveying and navigation, among other down-to-earth pursuits such as deciding what size monitor or television to purchase. The theorem also led to mathematical breakthroughs, such as calculus.
But who was Pythagoras, the person behind the famous and useful theorem?
Of Math and Mystics
Beyond the fact that he was born on the Greek isle of Samos around 569 B.C. and died around 475 B.C., not much is known about him. Pythagoras left no writings, but he did found a sect (or, what some would deem a cult): the Divine Brotherhood of Pythagoras. Its followers are often referred to as simply the Pythagoreans, a secret society dedicated to a combination of scientific and mystical precepts.
They were an eccentric bunch, and the legends surrounding Pythagoras and his followers are delightful. It’s said that Pythagoras refused to eat beans, and would not allow his followers to do so, because he thought beans had souls. The Pythagoreans were also said to be highly suspicious of sex, and according to Jordan Ellenberg in his book How Not to Be Wrong: The Power of Mathematical Thinking, they may have believed Earth had a twin planet on the other side of the sun.
Some of Pythagoras’ followers, it has been said, believed that he was a god. Yet they are also said to have tossed him into the sea and left him to die because the Pythagorean theorem was too, as we might say today, disruptive.
While that last myth is as unlikely as the others — and the poor sod thrown overboard is usually identified as Hippasus of Metapontum, another Pythagorean, rather than Pythagoras himself — it is certainly fitting, considering the impact of the theorem. It was dangerous, at least to the Pythagorean worldview. In working out that specific properties of a triangle, Pythagoras had stumbled upon the existence of irrational numbers. And that was a big problem.
'All Is Number'
The basic tenet of Pythagoreanism was that numbers are the essence of everything, as declared in their motto: “All Is Number.” They had some good reasons for looking at things this way. They were the ones who worked out that musical intervals corresponded to the lengths of the strings on a stringed instrument, and they had derived the golden mean, or golden ratio, from examining patterns in nature, such as nautilus shells and the petals of flowers.
As David Foster Wallace explains in Everything and More: A Compact History of Infinity, the Pythagoreans’ “attempts to articulate the connections between mathematical reality and the physical world were part of the larger project of pre-Socratic philosophy, which was basically to give a rational, nonmythopoeic account of what was real and where it came from.” They wanted to figure out how things worked — absent gods with thunderbolts — and everywhere they looked, they found numbers.
Prior to the discovery of the Pythagorean Theorem, the Greeks thought all numbers could be expressed as either a whole number or a fraction — a ratio of two whole numbers. But the Pythagorean theorem blew a big hole in that notion. Hiding in plain sight in the theorem was something very disturbing. If, for example, you look at a right triangle with two sides of 1 inch (or foot, or some such), the hypotenuse is a number the square of which is 2.
So what’s the square root of 2? Something the Pythagoreans couldn’t deal with: an irrational number; that is, a number that can’t be written as a fraction (or ratio). To us, this just means that the math is a bit more challenging (OK, maybe a lot more challenging). To the Pythagoreans, it was a challenge to their entire worldview, which was built on the supremacy, even divinity, of numbers that did not do such weird things.
Of course, now we have all kinds of weird numbers: imaginary numbers, transcendental numbers, the truly disruptive zero, plus quantum mechanics. And we muddle along more or less fine — even managing to make airplanes fly and invent computers.
Older Version of the Theorem
Writings by other members of the society were often attributed to Pythagoras himself, rather than the actual writer, presumably out of respect (or maybe as a form of self-defense). So it’s really not fair to pin all the oddity or all the credit on Pythagoras.
Much of what we attribute to Pythagoras could well be the work of another or multiple Pythagoreans. But real or composite, Pythagoras was not the first to figure out the famous ratio. Clay tablets found in what is now central Iraq show that Babylonian mathematicians were aware of the basics of the famous theorem at least 1,000 years before it freaked out the Pythagoreans. We don’t know how the Babylonians responded, but we can hope they resisted pushing anybody off a boat.















