At Long Last, Hobbyist Discovers "Einstein" Tile

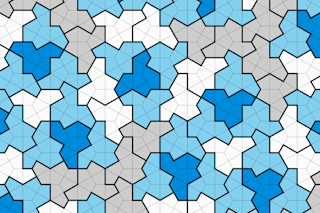
In his free time, David Smith designs tiles. More specifically, the retired print technician and recreational mathematician pieces together as many tiles as he can (no gaps allowed) before the pattern either repeats or cannot continue.

Until recently, every shape anyone had ever tested met one of those two fates — despite the scrutiny of many brilliant minds over the past 50 years. Then, one day last November, Smith found the only known exception.

Using an app called PolyForm Puzzle Solver, Smith constructed a jagged, 13-sided shape. Vaguely reminiscent of a top hat, he began filling the screen with copies of it. They joined seamlessly and, to his surprise, without repeating.

“The tessellations were something I had not seen before,” he says.

Keen to investigate further, he cut out dozens of paper copies and started fresh. One after another, the tiles kept falling into place. They invited him deeper into a striking visual pattern — and as it grew, so too did his excitement.

He showed this promising creation to Craig Kaplan, a computer scientist at the University of Waterloo. “Almost immediately it looked like he was onto something new and profound,” Kaplan says.

Though it took a while longer to prove mathematically, their instinct was sound: As they and two other colleagues announced in March, in a paper that has yet to be peer-reviewed, Smith had stumbled upon the long-sought “einstein” shape.

As used here, the word “einstein” has nothing to do with a certain German physicist. Instead, it evokes the literal meaning of his last name: “one stone.”

It’s a less yawn-inducing moniker for what is technically known as an “aperiodic monotile” — a single tile that can fill the infinite plane, on and on for eternity, in a pattern that never repeats.

On a typical bathroom floor, you’ll find clean-cut squares, triangles or hexagons, arranged in some clearly visible order. Now, picture those neat rows replaced by an apparently random jumble of blocks, and voila — aperiodic decor.

In other words, there is no section you can cut and paste to complete the rest of the tiling.

Before the 13-sided “hat” revealed itself to Smith, it was anyone’s guess whether an einstein even existed.

Mathematicians have been hunting for one since 1966, when Robert Berger devised the first set of tiles that could be laid out aperiodically. This was a landmark innovation but, with an unwieldy 20,246 distinct shapes, it was not yet a viable option for DIY home renovators.

As the quest continued for more elegant combinations, that number shrank from quintuple to single digits in just a few years. Before long, the monotile seemed within reach.

In 1973, Oxford mathematician and physicist Roger Penrose set the bar at two tiles — by organizing a pair of shapes called kites and darts in aperiodic fashion. But then progress stalled, and the final challenge stood for five decades.

Read More: How a Mathematician Solved a Problem That Puzzled Computer Scientists for 30 Years

After so much time, it may seem astonishing that an amateur beat the professionals to the finish line. In fact, Smith wasn’t even searching for an einstein. He attributes his success to “persistence mainly,” and perhaps a bit of luck, “although I feel like I was the chosen one,” he says.

Marjorie Senechal, a professor emerita at Smith College who has studied tiling since the 1970s, notes that the field’s history is strewn with contributions from untrained tinkerers. Most notably, around the time Penrose unveiled his kites and darts, a hobbyist and mail sorter named Robert Ammann independently invented a strikingly similar solution.

“This is a subject where you can literally get your hands on it,” says Senechal, who profiled Ammann in 2004 for The Mathematical Intelligencer. “If you have a good eye and an inquiring mind, you can find things that other people trying to work through theory can’t find.”

Smith’s ingenuity set things in motion. But because we’re dealing with an infinite plane, no amount of fiddling with finite tiles can guarantee the pattern won’t eventually start over.

The only path to certainty? Mathematical proof. So, Smith and Kaplan enlisted two more experts: Chaim Goodman-Strauss, a mathematician at the University of Arkansas, and Joseph Myers, a British software engineer.

Actually, aperiodicity is child’s play. Plain old rectangles can satisfy the non-repeating requirement, even though you could easily reassemble them periodically.

The real trick is to find a shape that only works aperiodically, one with just the right balance of complexity — enough to disrupt periodic pattern, but not so much that all pattern degenerates.

“That’s the magic that makes aperiodicity interesting,” Kaplan says. “They have to do a very careful dance between order and chaos.”

Read More: Is It Actually Impossible to “Square the Circle?”

To make sure the hat hit that sweet spot, Myers first employed a tried-and-true method, pioneered by Berger himself.

It begins with a set of “metatiles,” simple polygons that roughly resemble small groupings of hats. From there, you can combine metatiles into supertiles, supertiles into supersupertiles, and so on to the endless reaches of infinity.

Their paper demonstrates that this hierarchy is the only way to tile the plane with hats, which amounts to proving that the shape will never slip into periodicity. But then Myers forged a new kind of proof, and to understand it we’ll need to break the hat down into its basic parts.

Exotic as the shape appears, it’s well known to geometers as a polykite; start with a hexagon, draw three lines connecting opposite sides at their midpoints, and you wind up with six kites.

Combine two or more of these, and you get a polykite. Slap together eight in an especially fortuitous order, and you get a groundbreaking mathematical discovery. As the team writes in their paper, “the shape is almost mundane in its simplicity.”

Read More: The Shape of Madness

The hat’s 13 sides come in two lengths, and Myers realized that by adjusting the length of either set, he could create new shapes with the same properties. That means there’s not one einstein — but an infinite family of them, each morphing into the next along a vast spectrum.

At the two extremes (where the long and short sides disappear) and at the midpoint (where they become equal) lie periodic shapes, which can be used to establish the aperiodicity of the rest.

This intriguing addition to the repertoire of tiling proofs gives mathematicians something to chew on, but Senechal explains that it has roots in a more traditional strategy.

“There are connections to long-standing theory,” she says. “This situates their work in a continuum not just of tilings, but of thoughts about tilings.”

By the mere fact of its existence, the hat has settled one mystery. But it also raises new ones. Could there be more einsteins, for example, separate from this family? Senechal suspects there must be, and that this triumph could reinvigorate the search.

One of the most intriguing questions is the reason for its aperiodicity. The “special sauce” is still unknown, as Kaplan puts it: “I can’t point at part of the shape and say, ‘That’s why.’”

Nicolaas de Bruijn, a Dutch mathematician, eventually explained Penrose tiles as two-dimensional projections of a five-dimensional tiling. But as for a theoretical account of the hat, Kaplan says, “we’re not anywhere near that yet.”

It also remains to be seen whether this abstract curiosity will apply itself in the real world.

Read More: 5 Interesting Things About Albert Einstein

It may, of course, have a promising future in interior design — especially considering how snugly it fits against a grid of hexagons. It begs to be arrayed on the kitchen floor; anyone with hexagonal tiling and enough determination could trace the pattern themselves.

Many aperiodic tiles run roughshod over an orderly background, “but this one,” Kaplan says, “just kind of sits there very nicely. It’s almost ridiculously well-behaved.”

Supposing the hat does find its way to your local Home Depot, keep in mind that periodic arrangements are not for the faint of heart.

“If you just proceed blindly,” Kaplan says, “you’re probably going to get stuck.” And if by some miracle you find a contractor willing to humor you, “there’d be a lot of labor costs.”

Read More: How Mathematicians Cracked the Zodiac Killer’s Cipher