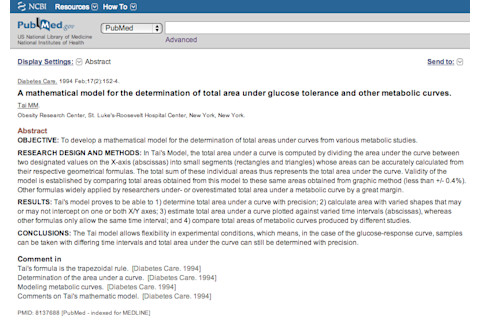
Photo: flickr/kawaiikiriThis is probably a good lesson for anyone - if you're a doctor, not a mathematician (dammit Jim!), and you think you've invented a new mathematical model for something basic like finding the area under a curve, you should probably run it by a mathematician before you publish it. She'll tell you that yes, your idea of using the area of lots of tiny rectangles to approximate the overall area under the curve is a very good one. In fact, it's called the trapezoidal rule, and it's part of the Newton-Cotes formulas. As in, Isaac Newton. But nice try!A mathematical model for the determination of total area under glucose tolerance and other metabolic curves. “OBJECTIVE: To develop a mathematical model for the determination of total areas under curves from various metabolic studies. RESEARCH DESIGN AND METHODS: In Tai’s Model, the total area under a curve is computed by dividing the area under the curve between two designated values on the X-axis (abscissas) into small segments (rectangles and triangles) whose areas can be accurately calculated from their respective geometrical formulas. The total sum of these individual areas thus represents the total area under the curve. Validity of the model is established by comparing total areas obtained from this model to these same areas obtained from graphic method (less than +/- 0.4%). Other formulas widely applied by researchers under- or overestimated total area under a metabolic curve by a great margin. RESULTS: Tai’s model proves to be able to 1) determine total area under a curve with precision; 2) calculate area with varied shapes that may or may not intercept on one or both X/Y axes; 3) estimate total area under a curve plotted against varied time intervals (abscissas), whereas other formulas only allow the same time interval; and 4) compare total areas of metabolic curves produced by different studies. CONCLUSIONS: The Tai model allows flexibility in experimental conditions, which means, in the case of the glucose-response curve, samples can be taken with differing time intervals and total area under the curve can still be determined with precision.”
Related content: NCBI ROFL: If you think you don't suck, you probably do
NCBI ROFL: Will your love last? This mathematical model may hold the answer…