The average person doesn’t spend a lot of time thinking about black holes, which is why a place like the Black Hole Initiative (BHI) exists. Founded in 2016 at Harvard University, it is the world’s first academic center devoted solely to the study of these fantastical, enigmatic objects.
After a BHI seminar last year, Harvard astrophysicist Ramesh Narayan talked with some colleagues — physicist Paul Chesler and philosopher and physicist Erik Curiel — about the inner structure of the black holes thought to litter the universe. Their conversation led to questions asked all too often at BHI: What would happen if you fell into a black hole of this sort? Where would you go and, more to the point, where would you die?
What distinguished this discussion from most at the BHI was that this time, Narayan, Chesler and Curiel resolved to actually find some answers to these enduring questions.

What would happen if you fell into a black hole? Where would you go and, more to the point, where would you die? (Credit: Composite, Alison Mackey/Discover; Black Hole, ESO/M. Kornmesser; Astronaut, Lia Koltyrina/Shutterstock)
Composite, Alison Mackey/Discover; Black Hole, ESO/M. Kornmesser; Astronaut, Lia Koltyrina/Shutterstock
Black Hole Bounties
They were by no means the first to delve into this issue. In 1915, Albert Einstein unveiled his general theory of relativity, encapsulated within 10 exceptionally complicated equations. They show how the universe’s distribution of matter and energy affects its geometry, or curvature, and how that curvature, in turn, is manifested as gravity.
Less than a year later, Karl Schwarzschild published the first solution (one of many) to those equations. It provided an explicit description of the gravitational field of an ideal configuration of matter: perfectly spherical, electrically neutral and non-spinning. If this mass were compact enough, Schwarzschild found, the sphere’s center would have a bizarre property: Its curvature and density would be infinite, resulting in what’s called a singularity, a literal wrinkle in the fabric of the cosmos.
Physicists consider such an object, now called a Schwarzschild black hole, to be an idealized concept. Actual stuff in the universe, including black holes, is always spinning, and has other imperfections, too.
It was not until 1963, nearly a half-century later, that the mathematician and physicist Roy Kerr came up with his own solution to Einstein’s equations, one that describes the space and gravitational field surrounding a real-life, rotating black hole — subsequently dubbed a Kerr black hole. However, when other physicists, building on Kerr’s result, tried to explore the crazy physics within these rotating maelstroms, they discovered some curious features.
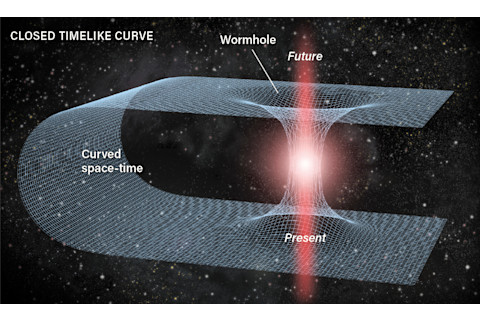
These included, according to Curiel, wormholes that could lead you out of the black hole and into another universe, as well as “closed timelike curves” — looping paths in space-time that would eventually take a traveler back to the time and place she began. It sounded like science fantasy, but Einstein’s and Kerr’s equations suggested that these were real possibilities.
Not everyone was on board with such fanciful features lurking within black holes. In fact, most physicists regarded them as “pathologies of the Kerr solution,” Chesler says, so unstable as to be effectively meaningless. “Like a pencil standing on its tip, if you disturb a black hole in the slightest way, those features will disappear.”
That, at least, was the presumption when he and his colleagues decided to carry out the first detailed numerical simulations of Kerr black hole interiors, building on the work of others in the field. With any luck, they’d figure out exactly what goes on inside.
As the rules of physics break down within black holes, unusual conditions could result in time travel. (Credit: Esteban De Armas/Shutterstock)
Esteban De Armas/Shutterstock
Getting to Work
They had their work cut out for them. “Although Einstein’s equations have been around for more than 100 years, they are horrendously difficult to solve,” Chesler says. Curiel calls them “probably the most mathematically complex equations in physics.”
Unlike the immobile, perfectly rounded Schwarzschild black holes, rotating black holes have bulges at their equators (just as Earth and the sun do). Because they lack the symmetry of a sphere, modeling them becomes a much more computationally demanding endeavor.
“The biggest thing we did to make the task doable was to spend much more time thinking about solving the problem than actually solving it,” says Chesler.
That meant determining the optimal choice of coordinates and coordinate system they’d use to describe their simulated black hole — literally, how they’d measure, model and navigate the space around it. Think back to high school math: You might use Cartesian coordinates when it’s convenient to represent points by their latitude and longitude (or x and y positions). But sometimes it’s easier to identify points by their polar coordinates — their distance and direction from a common origin.
Picking the proper coordinates and coordinate system is analogous to choosing the best directions and map before setting off on a road trip and knowing which landmarks to keep an eye out for along the way. A poor choice of coordinates could make the physics problem unsolvable, just as poor directions may not get you to your destination. A good choice of coordinates, on the other hand, can make the computational chore much more manageable.
After laying the groundwork, the researchers were ready to begin the actual simulation. “We start with the equations of general relativity,” Chesler explains, “specify some initial conditions, and then see how things evolve as we move forward in time.” The simulation worked out the geometry of space-time inside a Kerr black hole — about the same as determining the gravitational field, according to Einstein’s theory. Once the geometry had been established, the simulation could describe the trajectory of incoming light rays — essentially revealing the black hole’s interior structure. The whole computation was performed on a standard laptop with no special equipment. Chesler calls it “superb computing, rather than supercomputing.”
The Inner Truth
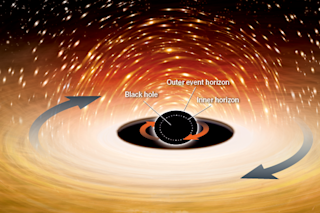
So what does this work — much of it described in a Physical Review D paper — reveal about the innards of a Kerr black hole? Like the non-rotating variety, a Kerr black hole has a central singularity and an invisible event horizon — a spherical surface of no return from which matter and energy can never escape. But a spinning black hole, unlike its stationary counterpart, has an “inner horizon,” too — a second surface of no return, also spherical and invisible, lying somewhere between the event horizon and central singularity. The faster the black hole spins, the closer the inner horizon is to the event horizon.
To visualize the inner horizon, consider this thought experiment: Imagine you could enter a spinning black hole and cross the event horizon while holding a flashlight that’s pointed outward. That light would eventually freeze along, or within, a spherical surface. That’s the inner horizon, Chesler explains: the point where the black hole’s gravity is strong enough to keep light from leaving, but not strong enough to drag it all the way into the center. The trapped light becomes so energized that it turns into a firewall of radiation, incinerating anything that passes through it.
The inner horizon is important for another reason, the BHI team concluded. If you were reckless or unlucky enough to get pulled into a Kerr black hole, “that’s where you’d die,” says Chesler. He compares crossing the inner horizon to “closing your eyes and driving into a brick wall.” Only in this case, it’s a wall of extremely curved space-time, tremendous gravitational forces and extreme radiation. For an intrepid traveler, the inner horizon represents the end of the line — a place you’d be instantly ripped apart and flash-fried, with your ashes dispatched at nearly the speed of light toward the central singularity. “It will not end happily,” Chesler notes. But it will end quickly.
And what of the hypothetical wormholes and other exotica that some researchers have speculated about? Wormholes, Chesler explains, “would be sealed off by the unboundedly large curvature of space-time inside the black hole.” It’s as if our universe were a giant, elongated balloon that is twisted until a knot, which is a kind of singularity, forms in the middle. “If you lived on one side of the knot, you couldn’t get through to the other side to reach the other universe,” Chesler says. In fact, there’d be no way of knowing whether another universe, or anything else, exists beyond that point. It effectively marks the end of geometry itself. Time travel would be ruled out, too, in this increasingly mundane picture of a black hole’s interior.
While that may disappoint sci-fi fans, the firewall the BHI trio discovered is a dramatic fixture in its own right — one that could deliver a slam-bang ending to many a tale of cosmic exploration. Plus, it finally provides an answer to the familiar question: What happens if you fall into a black hole?
Steve Nadis, a contributing editor to Discover and Astronomy, plays handball and volleyball in Cambridge, Massachusetts, where he lives with his wife, two daughters, and an unruly dog. This story originally appeared in print as "Taking the Plunge."