Last summer, Ken Ono of Emory University became a minor mathematical celebrity when he, along with collaborators Michael Griffin and Ole Warnaar, discovered four infinite families of identities — mathematical formulas involving variables (like x or y) that are true regardless of the values of those variables. (For example, (a * b)x = ax * bx..) The new identities are generalizations of two specific ones first found by the great mathematicians Leonard Rogers and Srinivasa Ramanujan in the early 1900s. The finding is a milestone in mathematics.
Discover: What led to your interest in the Rogers-Ramanujan identities?
Ono: I first learned about them from a famous story. In 1913, the great English mathematician G.H. Hardy received a letter from an unknown, uneducated clerk from India: Srinivasa Ramanujan. Attached were nine pages of mathematical formulas.
A lot of them were well known, and some wrong, but a few were gems, especially two. Hardy said that they must be true because no one would have had the imagination to invent them.
What were these special identities of Ramanujan’s?
They’re slightly more complicated versions of a beautiful “continued fraction”:
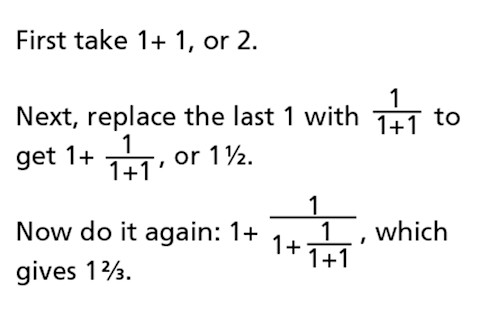
If you do that forever, you get the golden ratio, which is defined as:
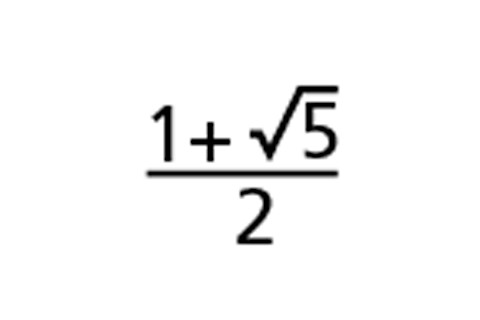
Ramanujan evaluated two other continued fractions in this way. It was largely because of those that Hardy, the professional, and Ramanujan, the amateur genius, ended up collaborating to invent some of the most important mathematics of their day.
How did Ramanujan come up with those identities that captivated Hardy?
Ramanujan had a secret device: two more identities that he had discovered, which later came to be called the Rogers-Ramanujan identities. He plugged specific numbers into those two identities.
What did you discover about the Rogers-Ramanujan identities?
Griffin, Warnaar and I found a framework that shows why they’re true and structurally what makes them tick. They turned out to be two golden nuggets that suggested the existence of a whole mother lode of identities out there. And we showed that they can easily produce numbers mathematicians call “algebraic,” which are rare, beautiful numbers akin to the golden ratio.
Why is it important?
The Rogers-Ramanujan identities are tied to a lot of deep mathematics. So this larger framework for them will open up new mathematical territory.
[This article originally appeared in print as "A Beautiful Find."]
