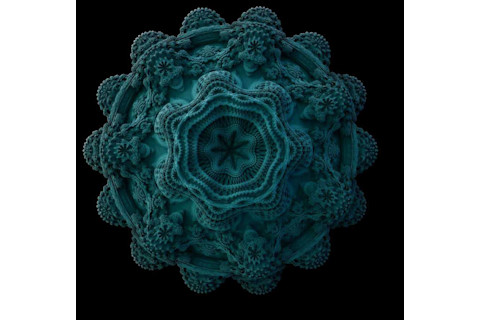
You might think that's an alien spore, or a crystal of some kind. But it's actually what appears to be a rendering of a three-dimensional fractal! Fractals are very interesting. There are different ways to describe one, but one way to think of one is that it's a shape that looks the same no matter what magnification you use. You can double it, triple it, make it 10,876,432 times bigger, and the object still displays (more or less) the same features. The term fractal was coined by Benoît Mandelbrot, and there is an entire subclass of fractals named after him. They are seen in nature (and art, like here) quite a bit. Coastlines are fractal, as are -- seriously -- some kinds of broccoli. However, fractals are generally calculated in two dimensions. What's new here is that the fractal pattern has now been calculated in three dimensions! That is, to say the least, a non-trivial procedure -- I used to play with some of the 2D equations many years ago, on my old 512k Fat Mac, with code written in Pascal (yes, with the semicolons and everything) and it was fascinating if very complex. But the 3D idea has been written up by Daniel White, who, along with others, figured out how to create and render such an incredible object. He even created a "fly-over" video to demonstrate the fractal pattern: Wow. Even if the math of this makes no sense at all to you, the beauty of this should be apparent. Which brings up a point: why are mathematical shapes beautiful? What makes them so pleasing to our eyes and brain; why did we evolve an appreciation for such things? I don't know, and at some point I'll have to research that a bit -- understanding the principles behind this will help me appreciate it even more.
Tip of the fractionally dimension hat to Fark.










