Mathematicians Find the Answers
Nice curves!
Dec 20, 2016 6:00 AMNov 12, 2019 5:59 AM
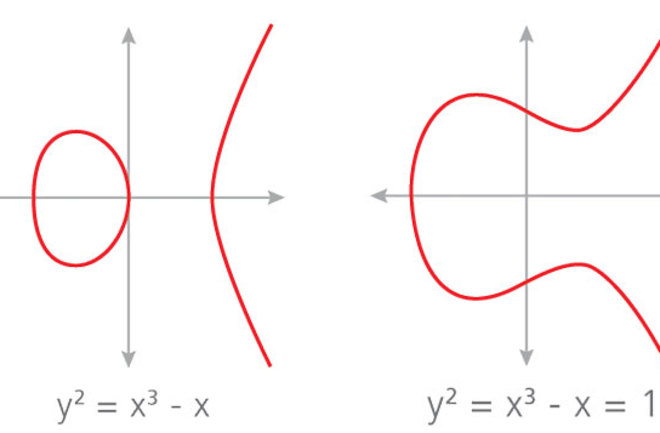
Certain algebraic equations can generate elliptic curves, useful in cryptography. | After Yassine Mrabet/Creative Commons 3.0
Newsletter
Sign up for our email newsletter for the latest science news
0 free articles left
Want More? Get unlimited access for as low as $1.99/month
Stay Curious
Sign up for our weekly newsletter and unlock one more article for free.
View our Privacy Policy
Want more?
Keep reading for as low as $1.99!
Already a subscriber?
Find my Subscription
More From Discover
Stay Curious
Subscribe
To The Magazine
Save up to 40% off the cover price when you subscribe to Discover magazine.
Copyright © 2025 LabX Media Group
