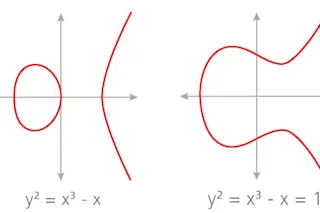
In high school, American students encounter a kind of wormhole connecting geometry and algebra: Geometric objects like circles and ellipses are linked to algebraic equations like y^2 = x^3 –x + 1. Students can visualize all the solutions to the equation as points in the circle — that is, each point in the curve represents a solution.
Make the equations slightly more complex, and instead of circles you get swooping loops and lines called elliptic curves. These curves have proven useful in creating cryptographic codes — and they have beguiled mathematicians with their complexity and beauty.
Each of those more complicated, curvy equations, however, has many solutions, and they can be wickedly hard to find. Mathematicians developed a trick for this: If they know a certain number of an equation’s solutions, they can use that wormhole between equation and curve to discover the rest of the equation’s solutions. The key ...