Whatever Happened to the Hole in the Ozone Layer?

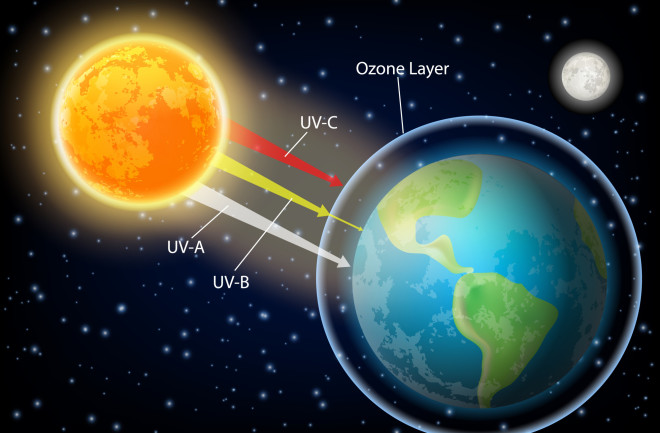
Almost 40 years ago, scientists discovered that human activities were depleting the ozone layer and that a hole had formed over Antarctica. These sobering discoveries brought the world together to tackle an environmental challenge of a lifetime.

Decades later, the ozone hole has come a long way since its dire outlook in the 1980s. But it's not a cause for celebration just yet. There are still ongoing efforts between policymakers and scientists to ensure the ozone in the atmosphere is protected. In light of the hole’s ongoing recovery, here’s a guide to how the hole formed, the coordinated effort to fix it, and whether it's likely to ever to take a turn for the worse.

Ozone, or trioxygen, is a highly reactive gas that’s composed of three oxygen atoms. You can find some ozone near Earth’s surface, but most is concentrated in the Earth’s stratosphere. At ground level, ozone is a poisonous molecule to humans and can damage the lungs when inhaled. Yet, it’s an essential and protective at 31 miles above the ground.

At the stratospheric level, it connects with other ozone molecules in a cover known as the ozone layer. These ozone molecules absorb UV radiation, acting as a sunscreen for life on Earth. In the 1960s and 70s, researchers began discovering that certain substances — particularly manmade industrial chemicals — disrupt ozone molecules. These substances break down ozone molecules by stripping away one of the oxygen atoms. Over time, these reactions can make the ozone layer less stable.

In 1985, this threat became known to the public. Scientist Joseph C. Farman and his colleagues discovered that atmospheric ozone over Antarctica had reduced by 40 percent. Certain human-made substances had reached the stratosphere and disrupted the ozone layer to the point of depletion, creating an extremely thin section commonly known as the ozone hole. The hole formed at the South Pole due to the region's unique meteorological and chemical conditions.

Scientists pinpointed the emissions of certain gases containing ozone-depleting substances as the main source of the problem. CFCs, short for chlorofluorocarbons, are one of the most detrimental gases to the ozone layer. CFCs contain chlorine — a compound that’s great for killing bacteria in swimming pools, and in its gaseous form is harmful to the ozone layer.

CFCs were widely used in previous decades, peaking in the late 1980s. Many refrigerators, air conditioners and foam-blowing equipment used to emit dangerous levels of chlorine gas into the atmosphere. Once chlorine reaches the ozone layer, ultraviolet radiation from the sun converts it into a reactive substance, which then destroys ozone molecules. Other compounds, such as bromine, have also played a role in depleting the ozone layer.

Even though levels of these substances in the atmosphere reduced drastically over the years, the ozone hole will only fully recover in coming decades.

Ozone layer thinning is a human health risk. That’s because more ultraviolet rays from the sun can pass through the layer and reach the Earth’s surface. Excess UVB radiation is particularly worrisome, as it can cause skin cancer and cataracts. UVB radiation also can harm marine life and plants, and reduce the productivity of rice, wheat and soybean crops.   

The effects of CFCs might go beyond the ozone layer. CFCs are potent greenhouses gases and could have a broader impact on climate change outcomes. CFCs are found in relative concentrations in the atmosphere when compared to carbon dioxide, so they’re considered a minor player in global warming.

While CFCs don't seem to cause global warming, a different picture emerges with regional warming. Recent research has shown that these same gases have sped up the warming of the Arctic, contributing to a sea level rise and surface warming in the North Pole.

Fixing the ozone hole is a matter of ensuring that no ozone-depleting gases reach the stratosphere. In 1987, the United Nations established the Montreal Protocol to regulate the quantities of these gases in the atmosphere. The Montreal Protocol was signed by 197 countries, and is the only UN treaty in history to achieve universal ratification. 

Over time, the protocol has been updated to include more substances that could cause harm to the ozone layer and the climate. For example, in 2016, hydrofluorocarbons were added to the list of controlled substances, because these gases have been identified as potent greenhouse gases. The treaty is considered to be one of the most successful protocols to tackle an environmental challenge caused by humans.

Yes and no. As a result of the Montreal Protocol, concentrations of ozone-depleting gases in the atmosphere have significantly declined. But according to Laura Revell, an environmental physics professor at the University of Canterbury, the issue isn't solved yet. “As long as the ozone hole continues to form each winter and spring, I don't think we can say the issue is fixed. We need to keep monitoring the ozone layer to check that it is recovering from the effects of CFCs,” she says.  

Although the gases have been banned, they’re not gone for good. Stephen Montzka, a research chemist at the National Oceanic and Atmospheric Administration, says they've detected possible illegal CFCs in the atmosphere. In 2018, Montzka coauthored a report in Nature that showed unexpected levels of CFC-11, a type of chlorofluorocarbons, were present. This concentration of CFC-11 was perhaps the result of unauthorized industrial production, going against the Montreal Protocol.

Further research by Montzka showed that the recovery of the ozone hole could be delayed because of these emissions. Despite this, Montzka doesn’t believe that the ozone layer is facing a significant risk from CFCs. “The enhanced levels of CFC-11 that we have noted in the atmosphere represent an amount that will not by itself cause substantial additional harm to the ozone layer if those levels diminish and return to [expected amounts] quickly,” he says.

As countries continue to abide by the Montreal Protocol, climate models show that ozone levels should return to standard measures by the end of the 21st century. "We need to be vigilant about adhering to the Montreal Protocol, even one country flouting the rules could delay ozone recovery substantially,” Revell says.