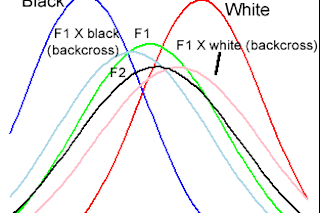
I generated the figure at left from table 9.6 in The Genetics of Human Populations. This book was published in 1971, but I purchased the 1999 edition (which was simply a republication of the original text by Dover) in 2005.* At the time I recall reading the section on inferring the number of genetic loci implicated in the variation in pigmentation with some mild skepticism. The authors, L. L. Cavalli-Sforza and W. F. Bodmer pegged the black-white difference due to ~4 genes. Their data set consisted of individuals of various races in Liverpool; whites, blacks, people with one white parent and one black parent (F1 hybrids), people with three grandparents of one race and one of another ("backcrosses," where you take an F1 and mate them with one of the parental lines), and finally, F2 individuals who are the product of pairings of F1s.
To come to the estimate the authors made some assumptions. For example, they assumed that blacks and whites were disjoint on the genes which encoded skin color in terms of their variants. Because these two populations lay at the opposite poles of the phenotypic distribution for humans it's a natural assumption, but they had nothing to go on besides their hunch at the time. It turns out though that to a good first approximation this is actually a valid assumption. If you assume that the two populations are fixed at the allelic variants, that they don't have segregating alleles which encode variation, then whites and blacks should exhibit the same variance due to environmental forces. This is what the authors saw. Using skin reflectance measures it seems that blacks and whites varied the same amount about their mean. If the two populations are approximately homozygote then the F1 generation, which are heterozygotes, should be between the two parental populations in trait value, but not exhibit much greater variance. Recall that they'd inherit a black and white copy at every locus. Therefore, all the variance in this population should also be environmental, rather than genetic. The real action comes in the backcrosses and the F2 generation. In these two populations segregation will result in a genetic variance component which will inflate the total variance. Therefore, genetic variance on this trait can be estimated like so:
Genetic variance = Total variance - Environmental variance
Recall that we already estimated environmental variance earlier. So genetic variance can be inferred by subtraction. Why do we see this pattern? Think about what happens when F1's cross at a single locus. They're heterozygotes. 50% of their offspring will be of like genotype. But 50% will revert back to one of parental genotypes. This naturally results in increased variance. Similarly, with a backcross 50% of the offspring will be heterozygotes, while 50% will be homozygotes.
Now let focus on a term, a, which defines the additive effect of a variant. It turns out that for their data set they didn't see any dominance effect, so the model is rather simple here where you have an environmental component, and an additive genetic component. The variance of this is:
Va ~ 1/2 ∑a2, 1/2 × the sum of a2
As per your model you can replace the sum by a multiplicative factor, the number of genes which produce the additive effect, k, and turn the additive effect into a mean. So you have:
2Va ~ k × mean(a)2
Now, recall that we have the mean values for whites and blacks. 1/2 of the difference between these is equal to:
k × mean(a)
In this system so far we know a, and we know the mean values for the parental populations. What we don't know is k. So we need to set up the equation so that k is the unknown which we're computing with the values we have. Some algebra leads to this formula:
k = [1/2(mean value white - mean value black)]2/(2Va (if you put k × mean(a) into the numerator in the right spot you can get 2Va to work out)
From their values:
k = (0.098)2 /(2 × 0.001215) ~ 4
k ~ 4 means that they estimate from the variance of effects there are 4 genes. When I first saw this I thought that the result was rather crude. But it turns out they were about right! In some ways they got lucky; pigmentation is notoriously large effect 'polygenic' trait. But it's still rather awesome to se that old genetic methods can yield answers which are validated in our time.
Addendum: Just to be clear, some of the data here is really rough & ready. The inference of 4 genes has a huge error due to small sample sizes in some of the sets (e.g., F2). And yet it turned out they were about right! Some of this may have been luck, but in this case the trait really was only barely polygenic.
* I just pretended that the trait was normally distributed, which probably overestimated the standard deviation, producing more overlap than is empirically justifiable.